Big O Notation Simplified
Source: Geeks for Geeks
In this blog post, I am going to talk about Big O Notation. I will explain what is the Big O Notation, how is Big O Notation associated with Algorithms, and provide some examples.
What is the Big O Notation?
Big O Notation is the language we use to describe the time complexity of an algorithm. Algorithm is a fancy term that programmers used to refer to functions. Big O notation is a convenient way to describe how fast an algorithm is growing with respect to the input. With Big O Notation we express the runtime in terms of how quickly it grows relative to the input, as the input gets larger.
Let me clarify:
How quickly the runtime grow : It’s hard to describe the exact runtime of an algorithm because it depends on other things such as the speed of your computer, what else the computer is running, etc. So instead of talking about the runtime directly, we use big O notation to talk about how quickly the runtime grows.
Relative to the input : If we were measuring our runtime directly, we could express our speed in seconds or minutes. Since we are measuring how quickly our runtime grows, we need to express our speed in terms of something else. With Big O Notation, we use the size of the input, which we call “n”. So we can say things like the runtime grows “on the order of the size of the input” (O(n)) or “on the order of the square of the size of the input” (O(n²)).
It does this with regard to “O” and “n” , where:
O refers to the order of the function, or its growth rate.
n is the length of the array.
As the input gets large: Our function may have steps that seem expensive when n is small but are excelled eventually by other steps as n gets larger. For Big O Notation analysis, we care more about the stuff that grows fastest as the input grows, because everything else is quickly excelled as n gets very large.
Examples:
This algorithm runs in O(1) time (or “constant time”) relative to its input. The input list could be 1 element or 1,000 elements , but this algorithm would still just require one “step”.
This algorithm runs in O(n) (or “linear time”), where n is the number of elements in the list. If the list has 10 elements, we have to print 10 times. If it has 1,000 elements, we have to print 1,000 times.
Here, I have nested loops. If our list has n items, our outer loop runs n times and our inner loop runs n times for each iteration of the outer loop, giving us n² total prints. It runs in O(n²)(or “quadratic time”). If the list has 10 elements, we have to print 100 times. If it has 1,000 elements, we have to print 1,000,000 times.
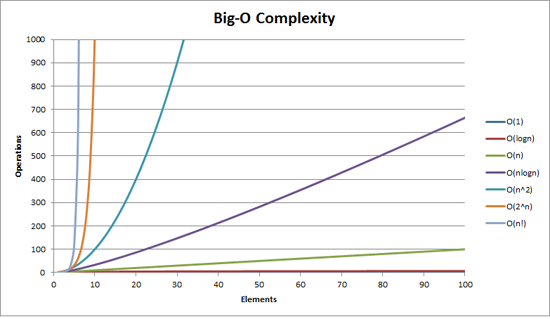
O(n log n) is really good
Big 0(n log n) scales very well, since logarithms grow very slowly.
log2 1,000 ≈ 10
log2 1,000,000 ≈ 20
log2 1,000,000,000 ≈ 30
In fact, Big O(n log n) time complexity is very close to linear — it takes twice the time to solve a problem twice as big .
Graph that represents the time complexity.
Graph that represent the time complexity
0(n2) is pretty bad
Algorithms with time complexity 0(n2) are useful only for small input: n shouldn’t be more than a few thousand.
10,000 ^ 2 = 100,000,000
An algorithm with quadratic time complexity scales poorly — if you increase the input size by a factor 10, the time increases by a factor 100.
Studying Big O notation makes you understand the very important concept of efficiency in your code. So when you do work with huge data sets, you will have a good sense of where major slowdowns are likely to cause errors, and where more attention should be paid to get the largest improvements. This is also called sensitivity analysis, and is an important part of solving problems and writing great code.
Sources: